NPR 新闻里又在讨论禁枪，原因是这个月的五角大楼枪击案。经过排查，发现犯罪嫌疑人用的手枪是田纳西警察局收缴又卖给 dealer ，然后几经辗转，到了犯罪嫌疑人的手上。新闻讨论的一方主张禁枪，另一方反对禁枪，理由其实也已经很古老 —— 即使禁枪，犯罪分子也总能搞到枪，而善良的市民由于没有枪支的保护，反而会变得更加危险。虽然这个观点很古老，但是以前没有意识到的是，这样的论点仔细考证起来，在公元前一二四年汉代的一次廷议上就有了。
《通鉴·汉纪十一》：“（公孙）弘尝奏言：‘十贼彍弩，百吏不敢前。请禁民毋得挟弓弩，便。’上下其议。”
因为弓弩的杀伤力太大，所以丞相公孙弘请禁弓弩。汉武帝把这条建议让大臣讨论。有一位侍中反对禁弓弩，理由是：
且所为禁者，为盗贼之以攻夺也；攻夺之罪死，然而不止者，大奸之于重诛，固不避也。臣恐邪人挟之而吏不能止，良民以自备而抵法禁，是擅贼威而夺民救也。窃以为大不便。
大意也是说，盗贼本来就是作奸犯科之人，你就是禁了弓弩，他们也会不顾禁令，不顾惩罚去持有弓弩，倒是普通遵纪守法的良民，会遵守法律不再持有弓弩，也失去了保护自己的手段，这样一来，盗贼会更加作威作福，而普通百姓则会遭殃。讨论的结果：汉武帝决定不禁弓弩，和现在美国的情形一样。
关于禁枪的问题，应该是犯罪学研究的问题，没有读过相关的文献，不知道数据的支持怎样，但是从理论上讲，倒是觉得禁枪和枪械犯罪率可能会存在一个非线性关系，i.e. 我们不把禁枪当做一个 binary choices（禁与不禁），而是把它当做一个连续变量，用政府禁枪的 efforts 来度量（譬如在禁枪上的 budget），这样禁枪与枪械犯罪率可能存在一个如下的关系：
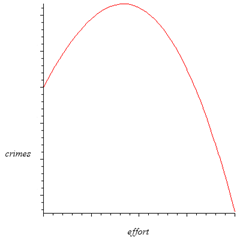假设没有 effort constraint (譬如 budget constraint)，政府没收所有在民间的枪支，那么枪械犯罪数肯定会触及 x 轴，也就是说犯罪数为零 ，但是由于 constraint 的存在， effort=< max_effort（无论是财政上的，还是制度，法律，政治上的），特别是 f(effort=max_effort)>=f(effort=0)，（f()是图中effort和 crimes 之间的函数），那么任何花费在禁枪上的 effort 都是白费，不能使犯罪率升高，而更进一步，当 max_effort 小于 f’(effort)=0 的哪一点（就是图中的顶点），那么任何禁枪的努力都会增加枪械的犯罪率——正如那个古老的观点，良民缴枪，邪人继续持枪。
换句话说，公孙弘和那位侍中的观点其实不矛盾，关键是朝廷有多少可支配资源，以及肯花多少资源（上面一直在讨论充分条件，而不是必要条件）……
不胡扯了，继续算我的 stochastic growth model 去了 —— 这是一个运气活儿，closed-form solution 唯一的算法就是 guess & verify，要靠撞大运，可是今天的运气不佳，sigh 。。。