大西洋城

更新：有一个错误，算 risk-adjusted 的 payoff，其实类似于 Sharpe Ratio, significantly different from zero 没有什么实际意义，至少要 significantly 大于 1 才算是 reasonable 的 strategy ：） -- July 24, 2011

三月份的时候路过拉斯维加斯去国家公园旅行，发现了一种新的自动机械轮盘赌，虽然在停留时间短暂，但是仍然在这台机器上赚了不少钱，于是想到了一个古老的问题：Gambler’s Fallacy (GF)

举个 GF 的例子，譬如一个 fair coin （这个假设很重要），如果连续仍了10次，都是正面朝上，那么当我们扔第十一次的时候，是不是更可能出现背面呢？如果你认为背面出现的概率会更大一些，这就是 GF 了，因为基础的概率学告诉我们，每次投掷都是独立事件，第十一次投掷的结果正面和背面的概率仍然是相等的。

单单看这个例子本身没有什么太大的意思，但是同时我们从统计的角度看这个问题，因为大数定理的存在（i.e. 这个 process 是 mean reversion 的，你仍的次数足够的多，你的期望值趋近于 0.5 ），那很自然就会想到，如果我们不只是简单作单次的预测下注，而是从大量重复统计的角度上下注（赌反方向），那么我们的收益会不会比纯粹 uninformed 的投注（譬如随机投注，或者只压正面）要好？

需要强调的是，我们考虑的只是投注的策略，而不是做时间序列上的预测 (forecasting)，因为就预测而言，这是一个明显的白噪声过程。也就是说我们只考虑一个策略优化问题。

当然这既是一个 theoretical 的问题，也是一个 empirical 的问题，我们偷懒的只从 empirical 的角度看这个问题。

我们把问题简单化，只关注简单策略，也就说我们的策略必须是能用大脑计算的，否则即便是你通过收集这个自动机械轮盘赌的数据，发现了这个机械的 idiosyncrasy 导致投掷的结果出现统计规律，能用譬如一个 exponentially weighted moving average (EWMA) 来预测，但是你如果不能快速心算出你的策略，这也是没有什么实际意义的。

我们考虑三种策略，前两种是 uninformed 的，也就是说策略是独立于你新获取的信息的，最后一种是 informed的，策略是基于新获取的信息的。

第一种策略称之为 Odd Even Strategy (OES)，顾名思义，就是第一压正，第二次压反，第三次压正，重复直到赌博结束；

第二种策略称之为 Straight Bet Strategy (SBS)，也就是不管怎样，都只压正（或者压反）；

第三种策略称之为 Looking Back Strategy (LBS)，每次压住前往前看 m 个 periods，given 一个 threshold value rho (0.5<rho=<1), 如果这 m 个 periods 的 average 大于 rho， 则压 1 （譬如 1 表示正面），对称的，如果 average 小于 1-rho，则压 0。 如果条件不满足，什么都不压。假定 m =10，我们向前追朔10个periods （同时也符合一般轮盘赌提供的历史数据），利用一些简单的optimization 和 calibration,  大概估算 rho= 0.618。

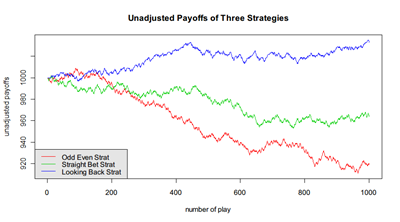
假设我们玩1000次，下注的时候每次下注 $1 ，我们的赌本是 $1000，三种策略的收益如下图：

上图的收益并不能说明什么，只是一个 realization，但是相对而言，第三种策略的标准方差相对比较小，原因之一是因为第三种策略并不是每次都下注，如果把图放大其实可以看到蓝色线条有很多“平顶”，这是不下注的时候。

基于这三种策略，我们作一个简单的蒙特卡洛模拟，结果见下表：

	n=10^4		n=10^5
	r-adj payoff	sd	r-adj payoff	sd
OES	-0.01797056	0.02302582	-0.006824031	0.007238402
SBS	-0.03311233	0.02290396	-0.01122852	0.007258676
LBS	0.1144682	0.02278219	0.1226927	0.00721828

 

上面提到 r-adj payoff 指的是 risk-adjusted final net payoff, 它是用每1000次轮盘赌的最终净收益除以这1000次轮盘赌收益的标准方差得到的（类似计算 Sharpe Ratio 的算法），n=10^4 是1万次模拟的结果，n=10^5 是10万次模拟的结果。模拟的结果说明：

1. Uniformed 的策略（OES，SBS）的风险调整净收益都不 significantly different from zero (at 5% significance level)。这和理论的预期是符合；
2. Informed 的策略（LBS) 的风险调整净收益是正的并且significantly different from zero。

也就是说这样简单的informed的策略是能够带来正收益的。注意这个策略只是告诉你什么时候下注，和如何下注，把它和其他一些特定的投注策略(譬如 modified  martingale betting strategy)结合，应该能够提供一些可观的收益，所以我们在拉斯维加斯赢的钱也不完全是运气。

这个结果同时一些 empirical observation 项符合：1）这种机器不是在每个赌场都有，只有拉斯维加斯的 MGM才有；2）这个机器前排队的人很多；3）这个机器很容易坏。

离我们的比较近的 Atlantic City 没有这种机器，所以在那里赌博，只能靠运气了，不过上周的运气不错：

哈哈，这样的小概率都让我撞上了，狗屎运：）

P.S. 这个问题也有很广泛的意思，譬如股票交易，比较 liquid 的股票的 log return 几乎肯定是一个白噪声（Fama 的 Efficient Market Theory，呵呵，不知道他什么时候能得诺奖），如果我们有 high frequency data，我们能否有一些策略，通过白噪声的 mean reversion 来获利？猜测是由于 transaction cost 的存在(bid-ask spread, commission fees) 上述 payoff 可能会小于零，因此没有太大的现实意义，但是赌博可以一试。

P.S. 希望上述的运算和模拟里面没有错误，有空会验算一下：）