vba

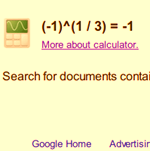一直好奇一个关于 power function 算法的问题，直到自己动手写 power function。

在不同的编程语言里，遇到过同一个问题：(-1)^(1/3) 是多少。 很显然，在实数集里，这个表达式是有意义的，正如右图 Google Calculator 给的结果，在实数集里，它等于 -1。但是在很多编程语言的实数集运算中，这个表达式是无意义的。

譬如在 C++ 里，用 cmath library, 当你计算 (-1)^(1/3) 时，你得到输出结果是：

 -1.#IND 

在 C#里，用 System.Math, 作同样的计算，得到的输出结果：

NaN

在 R 里，不使用复数集，得到的结果也是一样的：

[1] NaN

同样的在 VBA 里，如果不 call Excel的 power function ( i.e. Application.WorksheetFunction.Power) ，而是直接使用 ^, 得到的结果仍然是 run-time error. 其它的编程语言也类似。

在复数集中，如果用 MATLAB, 得到的结果：

 0.5000 + 0.8660i

用 Maple，结果：

.5000000001+.8660254037*I

用 R 的复数集(i.e. as.complex(-1)^(1/3))，得到的结果：

[1] 0.5+0.8660254i

很显然，所有的语言的 power function 用的是同一种算法。这种算法无法得到实数解，而复数解得到是同一个数值。因为 power function 太基本，虽然有疑问，但是也没有过多的想这个问题，直到后来用 Q。

Q 的语法和 C++/C#/JAVA，或者 MATLAB/R/MAPLE 都不太一样，"^" 符号的定义和 C++/C# 相同，不是 power function。刚开始用的时候，不知道 Q  的 power function 是 xexp，觉得 power function 又不难，自己写一个吧，但是真正开始写，却又卡壳了：(int，int) 的函数好写，那 (double, double) 的呢？

拿出算法圣经《 Numerical Recipe 》（第三版），但是却发现它没有给出 power function 的算法，大概是太基础了吧，所以自己又想了一下，幸亏 Q  里的 log 和 exp 还是 log 和 exp，后来就想到用

exp(y*log(x)) = exp(log(x^y)) = x^y

来定义 power function，解决非整数的问题。这样的以来，一般的问题都解决了，但是因为用到了 log(x) , x 的值必须非负（0 的问题可以很简单的处理），所以一旦 x<0，这个算法就不适用了 —— 这时才突然的想到莫非上面的那些问题的症结正在此？实数集的问题是由于 log(x), x<0 在实数集里无定义，那复数集呢？在 MATLAB 里试了

>> exp(1/3*log(-1))
ans =
   0.5000 + 0.8660i

果然是这样的。所有的算法都依赖于 log 函数来获得 power 函数的值，这导致了上述问题在实数集无定义，而在复数集因为 log（-1)  =  3.1416i  这个默认值，导致了 0.5000 + 0.8660i  这个结果。

但是问题还没有结束。看到 log（-1），自然想到了 2*log(i), 然后自然而然的想到傅立叶变换里常用的 trick 可以解出 log（-1）的一般表达式（为了省事儿，下面用 LaTex写了）：

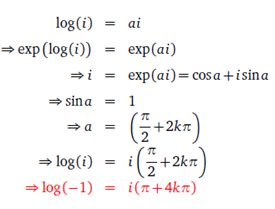
有了 log（-1）的通解，我们可以让 power function 获得任意 x^y, x<0 的所有解。譬如 (-1)^(1/3)简单测试一下，在 MATLAB 里，

x=2*i*(pi/2+2*(-3:3)*pi)
exp(1/3*x)

得到：

x =
        0 -34.5575i        0 -21.9911i        0 - 9.4248i        0 + 3.1416i        0 +15.7080i        0 +28.2743i        0 +40.8407i
ans =
   0.5000 + 0.8660i   0.5000 - 0.8660i  -1.0000 - 0.0000i   0.5000 + 0.8660i   0.5000 - 0.8660i  -1.0000 + 0.0000i   0.5000 + 0.8660i

结果里面包含了它的所有三个解。因为当 x<0, x^y = (-1)^y*(|x|)^y，所以只要有 (-1)^y ，就可以得到任何负数的 power function ( exp(a+bi）也可以用上面的方法转化成三角函数来解）。

上面的长篇累牍都起源于一开始的时候不知道 Q 的 power function 是 xexp，但是如果不是自己去写 power function，恐怕也没有机会搞明白 (-1)^(1/3) 这个简单的问题，俗谚云：“看人挑担不吃力，事非经过不知难。”诚哉：）

最先习惯的用的计量软件是 stata，然后是 vba for excel， 然后是 R，大概因为是这个学习路径，导致了在 R 中的一些不良习惯。 stata 的指令很多都是直接针对 vector 的，譬如下面的 panel data：

如果需要只需 CHN 的数据，在 stata 里只要：

keep if ID==”CHN”

就可以了。而 VBA 中因为 excel 表格的直观，一般是用 for  或者 do loop：

Sub chn()

n = Range("A50000").End(xlUp).Row

for i = n to 2 Step -1

if Cells(i,"A")!="CHN" then
Cells(i,"A").entiredRow.delete

end if 

next i

End Sub

因为 R 中的 if statement 不能直接针对 vector， 所以就习惯像 VBA 一样用 loop 来整理数据，但是因为 excel 中最大的数据量不过 6万五千多行 256 列，数据量并不大，所以用 loop 虽然慢，但是因为数据量的限制，还算能忍受，但是在 R 中，如果有上十万的 observations，再用 loop 就极其的痛苦了，虽然R中的loop 的效率要比 VBA 高（尽管不如 S），虽然刚换了 Duo Quad 的 CPU，但是仍然能算到死机 （虽然可以 remote access 学校的 cluster 上去，但是浪费学校的资源也不好），所以迫使自己重新学习 R 中的 vectorization，其实比如上面的例子，在 R 中用 vector 作也简单（假设上面 data frame 的名称是dat）：

chn<-dat[grep("CHN",dat$ID),]

也挺简单的。所以程序还是一个摸索熟练的过程 （ 虽然我还没有发现如何像 stata 一样便捷的在 R 中的 panel data 里创建 lag variable，并且还在等待大牛人们完善 R 中的 panel data package，譬如 fixed-effect negative binomial model，但是 R 的灵活性，特别是在编程和模拟上，还是超出其他软件很多，特别是 R 是 免费的！）

<

p>

因为需要从一篇旧的PDF格式的 proposal 中拷贝一些文字出来，又找不到生成 PDF 的 LaTex 源文件，所以不得不 ctrl+c & ctr+v，但是 PDF 的文字直接拷贝到 word 里格式就乱掉了，一行一行的清除 paragraph break 实在麻烦，用查找替换还要运行多次，所以就写了一小段 Word 中的 VBA，测试了一下，效果还不错，贴出来分享一下：

<

p>

因为句号加段落换行是段落结尾的必要条件，所以先将.^p 替换成 .^l 保护起来，然后把多余的换行全部转换成空格，然后再把.^l恢复成.^p，最后把段落的对齐设置成两端对齐（这是读惯了汉语的喜欢，喜欢方方正正的文字块）。

这个办法还可以扩展为可以识别问号或者感叹号结尾的段落，但是因为用的不多就没有加入，同时也可以修改用于汉语。以前有一个叫做 DreamEditor 的小软件（经常和 Cterm 一起打包）可以很方便的实现上述功能，并且功能更强大，但是已经很久没有更新了，所以在自力更生一下。