实证政治理论

台湾2012年选举结束，国民党胜出，在 维基百科上看到了投票的结果，很好奇蓝绿投票的地理分布，于是用维基百科上给的投票数据，又从网上找来了免费的台湾 GIS 数据，在 R 里自己画了一下。这个 GIS 数据比较古老，和现在台湾的行政区划略有不同，譬如嘉义县和嘉义市、新竹县和新竹市还没有分开，而高雄市和高雄县、台南市和台南县、台东市和台东县却是分开的，还有没有新北市，只有台北县（所以上图的 Taipei 图例其实是新北市，忘记改了，呵呵）。好在边界的坐标没有大变，所以手动的作了调整，毕竟是免费的 GIS。arcGIS要更精确些（包括边界的 polygon ），但是那个要钱的：）

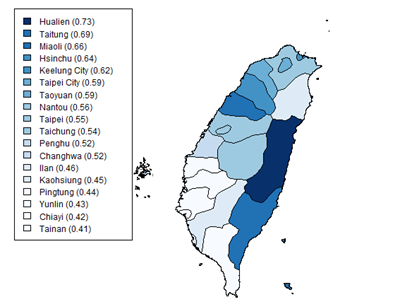
每个投票区域的“蓝”度由 蓝票/(绿票+蓝票) 的比例来决定，按照这个简单的算法，台湾版图上最蓝的是花莲，其次是台东和苗栗。最不“蓝”的是云林，嘉义和台南。图例的括号里的数字就是这个地区的“蓝”度。

从这个得票的地理分布和最终国民党和民进党最终 51.6% 比 45.6% 的得票率来看，民进党的竞选纲领有问题，明显的没有获得中间选民的支持，而是过于政策导向 (policy-oriented) 了。蔡英文的竞选过于侧重 base 选民，忽略了 swing 选民，失败也是在情理之中。不过有时候这确实也是一个很艰难的问题，如果不能得到 base 选民的支持，就无法从党内初选中胜出，参加最终的角逐。党内的 median voter 的 preference 如果和全部选民中的 median voter 的 preference 相差太远，不是一件好事。 同样的，就即将到来的美国大选而言，如果 Romney 能赢得初选，他对于 Obama 的威胁时最大的，但是正是因为他能和 Obama 争夺中间选民，反而使共和党内铁杆选民对他的支持减弱了，因为他会被认为不是真正的 conservative 。

下面是生成这副地图的 R  codes：

   1:  library(maptools)

   2:  library(RColorBrewer)

   3:  tw.map <- readShapePoly('taiwan/TWN_adm2.shp')

   4:  mcol=brewer.pal(9, 'Blues')

   5:   

   6:  votes = read.table('votes.csv',sep=",")

   7:  votes = votes[ ,2:5]

   8:  votes=votes[votes[,1]!="",]

   9:  votes

  10:  names(votes)<-c("loc","total","green","blue")

  11:  votes$bratio <- votes$blue/(votes$green+votes$blue)

  12:  votes$col <-floor(((votes$bratio-min(votes$bratio))/(max(votes$bratio)-min(votes$bratio)))*8)

  13:   

  14:  provname=votes[,1]

  15:  f=function(x,y) ifelse(x %in% y,votes[votes$loc==x,6],-1);

  16:  colIndex=sapply(as.character(tw.map$NAME_2),f,as.character(provname));

  17:  colIndex[c(1,15,17)] = colIndex[c(8,14,16)]

  18:  fg=mcol[colIndex+1]

  19:   

  20:  votes = votes[order(votes$bratio,decreasing = T),]

  21:  bkp=paste(as.character(votes$loc)," (",as.character(round(votes$bratio,2)),")",sep="")

  22:  plot(tw.map,col=fg)

  23:  legend("topleft", bkp,fill=mcol[votes$col+1], bty="o", cex= 0.75, pt.lwd=3)

世界杯踢完了。作为一个资深球盲，我开始认真看世界杯（的结果）是从 1/8 决赛开始的，因为从那时起，我开始在 BBS 上参与赌球活动：除了第一场赌输了以外（因为第一场是随便下注的），接连的六七场包括决赛都赌赢了，赚足了伪币。

当然，这届世界杯，只看章鱼保罗的预测就可以——但是这是事后诸葛亮，因为事前没有理由认为章鱼的预测都是准确的；并且作为赛先生的信徒，也无法说服自己信章鱼。所以作为球盲，赌球的决定其实是通过孔多塞的陪审团定理 （ Condorcet Jury Theorem, CJT）来完成的。

孔多塞是18世纪欧洲启蒙运动以及法国大革命时期吉伦特派的代表人物之一，后来被执政的雅各宾派拘捕，两天后死亡，他留下的 CJT 最初只是一个比较松散的定理，大致的表述为：

“在一些条件下，当面对两个选择并存在不完全信息时，多数人的选择总优于这些人中任何一个个人的选择，并且参与选择的人数越多，得到的结果越优。”

举个最简单的例子，假设一群淳朴的山民逃难，面前出现两条路，这群人里每个人多多少少都对这一带的自然环境有所了解，但是没人都确切的知道那条路更好走一些，这时由头人作出选择不如由大家一起投票的作出的选择更优，并且投票的人越多，得到的结果就越优。

CJT 里很容易看出德先生的影子 —— 没错，经过证明的 CJT 曾经被作为民主的数学基础，但是后来发现 CJT 中的“在一些条件下”的这些条件实在是太严格、太多限制以至于对于现实政治而言变得不切实际起来，所以社会选择理论\实证政治理论的先驱之一 Duncan Black 曾评价说对于民主政治，CJT 是一个 “truly … … an unpromising start” 。

【题外话，Black 是苏格兰人，虽然他是用数学方法研究政治的先驱者，并开创了经济学和政治学里一个很广阔的领域，但是当年他在英国却混得很惨。他的想法并不被人接受，而是被质疑和责难。他投往当时英国顶级期刊 The Economic Journal 和 Economica 的两篇 paper 都被无情的拒掉了，他那本书 The Pure Science of Politics 先后投给了四个英国的出版社，全部被拒；

而此时在大洋彼岸的美国，一个比他年轻十二岁的小伙子也在作者同样的工作，他就是后来名声如雷贯耳、拿了诺奖的 Kenneth Arrow。Arrow 的毕业论文 Social Choice and Individual Values 很顺利的就于1951年发表了，而此时 Black 的一篇 paper 正在 Journal of Political Economy 被审阅，事实上，他的这篇 paper 1949年就投了，但是被 JPE 压倒 51年才给结果—— JPE 的编辑和审稿人对 Black 说，你这篇 paper 和 Arrow 最新出的一本书的想法很相近，你应该做些更改，把自己的 paper 和 Arrow 的贡献联系在一起 —— 言外之意是说 Black 借鉴了 Arrow 的工作，应该给 credit。 Black 一怒之下就取回了投往 JPE 的这篇 paper 而是自费找了一家出版社自己出了本小册子 Committee Decisions with Complementary Valuations … … 顺便说一下 JPE 此时的编辑也是 Cowles Commission 的 Assistant Director of Research，而 Arrow 的毕业论文就是在 Cowles Commission 作的  …… 此一事足见学术界人脉的重要以及开创一个新领域的艰难。 PS，此八卦来源于芝大的诺奖得主科斯】

扯远了，CJT 对于民主政治的作用的有限，但是对于赌球却有莫大的帮助 —— 每次在 BBS 上赌球之前，在网上查了欧洲各大赌球网站的赔率，这些赔率基本上都一致，基于这些赔率在 BBS 上下注，毫无例外，全部都赢了 ——因此推测章鱼保罗的选择大概是饲养人员看了各大赌球网站的赔率后操纵的；

具体的说：赌球只有两个选择（足球毕竟是两个队踢的嘛），大部分赌徒对于每个球队多多少少都有些经验与信息，所以 CJT 的基本条件满足；

另外，CJT 要求“真诚投票”，这在赌博里是显而易见的，因为要用真钱下注，必然是 sincere voting；

CJT 要求信息获取的成本不能太大，否则会有人 free ride；赌徒中的大部分应该是铁杆球迷，他们对于足球的了解使得他们获取信息的成本不大，对于我这样的球盲，确实是 free ride 了，但是我并没有参与真正的赌球中，不影响能够低价获取信息的球迷的选择；

CJT 要求投票之间的关联性不能太强，网络赌球由于没有距离成本，参与者本身就是高度分散的，因此也基本上满足这个条件；

CJT要求投票者目标相同，赌球的人都想赢，没人专门是来向赌输的；

等等等等。所以按照 CJT 投注，对于球盲来说，确实是最优的选择，而事实也证明如此 —— 不过这只是一些直觉上的判断，并没有经过严格的数学证明 —— 也许严格的证明会有一些很有趣的结果，但是 。。。算了吧：）