Exception Handling & OOP in R
Submitted by kzeng on Thu, 2011-06-02 23:00 大概不同的学科会造就不同的思考方式,记得若干年前和LD走在加州 Albany (伯克利附近)有些破败的马路上,突然在一片空地上看到两只狗,LD脱口而出“两只”,我也脱口而出“活的”。所以LD是学理的,我是学文的。
大概不同的学科会造就不同的思考方式,记得若干年前和LD走在加州 Albany (伯克利附近)有些破败的马路上,突然在一片空地上看到两只狗,LD脱口而出“两只”,我也脱口而出“活的”。所以LD是学理的,我是学文的。
又好比为称赞人,学文的也许会顺口说道:“东陵虽五色,不忍值牙香。”,学理的会问:“这是说啥的?”;学文的会说:“这说的是瓜,用来称赞你的。”;学理的说:“这不是在骂人瓜娃子吗?”。。。学文的会暗自庆幸没有说:“浪乘画舸忆蟾蜍,月娥未必婵娟子”(“姮娥遂託身于月,是为蟾蜍”——张衡·《灵宪》)。
编程语言也是一样,不同之处是 epistemology 上的 (大概也只有学文科的人才会把 ontology, epistemology 这些东西挂在嘴边),就好比接触 C++ 以前从来没想到过 R 的程序可以如此这般如此这般的来写:例如以前从来没有想过 R 里的 (line by line ) debugging, exception handling , 以及 OOP 之类的东西。一个简单的例子,譬如突然想大致画一下任意股票期权的 volatility skew。
纯粹(旧的) R 式的写法:
1: library('quantmod')
2: library('RQuantLib')
3: x <- getOptionChain("AAPL",Exp ="2011-07-16")
4: optionVal <- as.numeric(x$calls[,2])
5: strike <- as.numeric(x$calls[,1])
6: getSymbols("AAPL",src="google")
7: n <- length(strike)
8: mtrty<-businessDaysBetween(from=Sys.Date(),to=as.Date("2011-07-16"))/252
9: under<-Cl(AAPL)[nrow(AAPL)]
10: imvol <- array(NA,n)
11:
12: for ( i in 1:n){
13: imvol[i]=EuropeanOptionImpliedVolatility("call", optionVal[i],under,strike[i],0,0.02,mtrty,0.2)$impliedVol
14: }
quantmod library 提供了直接从 Google, Yahoo 等来源读取金融数据的接口,RQuantLib library 是 QuantLib 在 R 里的 port。 imvol 是一个vector, 用来储存数值算法得到 implied volatility,但是因为这只是一个粗略的计算,数据中存在着一个很大的问题:underlying 的数据和 derivative 的数据不是 synchronous 的(high frequency 数据常有的一个问题),某个 strike 的 derivative 交易的频率比较低,所以它的价格滞后,不能体现出它的真正市场价格。也是因为这个问题的存在,我们在运行这段 code 时候很快就出现错误:
1: Error in EuropeanOptionImpliedVolatility.default("call", optionVal[i], :
2: root not bracketed: f[1e-007,4] -> [2.533890e+000,6.291277e+001]
因为 derivative 的价格和 underlying 的价格不是 syn 的,所以合理的 implied vol 的数值解不存在。程序因此中断,如果看 imvol 这个 vector:
[1] 1.331497 1.250151 1.481016 NA NA NA NA NA NA [10] NA NA NA NA NA NA NA NA NA [19] NA NA NA NA NA NA NA NA NA [28] NA NA NA NA NA NA NA NA NA [37] NA NA NA NA NA NA NA NA NA [46] NA NA NA NA NA NA NA NA NA [55] NA NA NA NA NA NA NA NA NA [64] NA NA NA NA NA NA NA NA NA [73] NA NA NA NA NA
只有三个有效值,后面的值全是 initialize 的 missing values。按照旧的方法,debug 找出出现问题的地方,逐一处理,但是这样很麻烦,有时候也没有必要。所以就想到借鉴 C++ exception handling 的 try - catch方法,如果出错,我们 throw 一个 exception,然后继续其余部分的 code。R 里面也有类似的方法,所以我们可以重新写这个 loop:
1: for ( i in 1:n){
2: result<-try(EuropeanOptionImpliedVolatility("call", optionVal[i],under,strike[i],0,0.02,mtrty,0.2),silent =TRUE)
3: if(class(result) =="try-error") next
4: else {imvol[i]=EuropeanOptionImpliedVolatility("call", optionVal[i],under,strike[i],0,0.02,mtrty,0.2)$impliedVol}
5: }
在上面的 code 里我们作了一个简单 exception handling,先 try implied volatility 的数值解,把结果定义为一个叫做 result 的 object,如果出错,那么 result 应该属于 try-error 这个 class,所以我们作一个简单的判断,如果出错了,就直接 next 跳过。最后我们的 imvol vector 是:
[1] 1.3314972 1.2501506 1.4810157 NA NA NA 1.0397009 NA [9] NA 1.0749333 NA 0.9936863 NA NA 0.7165703 NA [17] NA NA NA 0.4677549 NA NA NA 0.5650445 [25] NA NA 0.4720218 0.2539875 0.3110036 0.2952723 0.2441016 0.2276886 [33] 0.2379125 0.2209396 0.2250593 0.2162720 0.2144386 0.2117865 0.2078974 0.2044520 [41] 0.2014596 0.1984621 0.1990857 0.1978392 0.1984587 0.1999078 0.2007216 0.2027609 [49] 0.2042993 0.2119021 0.2126273 0.2281725 0.2231475 0.2280039 0.1892973 0.2453698 [57] 0.2485359 0.3305246 0.3448491 0.2755123 0.2963304 0.3480423 0.3299750 0.3087564 [65] 0.3814543 0.3350278 0.3369351 0.4618993 0.3985197 0.3226662 0.4635653 0.3968701 [73] 0.3984441 0.4608958 0.3962065 0.4239336 0.4901043
尽管中途出错,但是仍然不会中断我们的 loop。
更进一步,我们可以像 C++ 一样在 R 里定义 class 和 相应的 method,从而进一步提高 code 效率(主要是 reusability ,这也是 OOP 的主要目的之一)。R 里有两种定义 class 的方式,一种旧的 S3 class,一种是新的 S4 class。 这里用 S3 作为例子,我们首先定义一个 impvol class 和它的 constructor:
1: impvol<-function(tick, exp="2011-07"){
2: getSymbols(tick,src="google",from=Sys.Date(),to=Sys.Date())
3: under <- as.numeric(Cl(get(tick)))
4: x <- getOptionChain(tick,Exp =exp)
5: optionVal <- as.numeric(x$calls[,2])
6: strike <- as.numeric(x$calls[,1])
7: option<-cbind(strike,optionVal)
8: impvol<-list(tick=tick,
9: exp=exp,
10: under=under,
11: option=option)
12: class(impvol)<-"impvol"
13: return(impvol)
14: }
R 的 class 的定义和 C++ 还是有区别的,在 R 的 class 里面,我们只定义了它的 member variables ( tick, exp, under, option ),和它的 default constructor. 它的 method 并没有在 class definition 里 declare。定义了这样一个class 之后,我们就可以方便的获取任意stock 的数据了,譬如:
1: s1 <- impvol("F")
我们初始化一个关于福特的 impvol class 的object,把它定义为 s1 ,然后我们得到:
1: > s1
2: $tick
3: [1] "F"
4:
5: $exp
6: [1] "2011-07"
7:
8: $under
9: [1] 14.18
10:
11: $option
12: strike optionVal
13: [1,] 10 4.30
14: [2,] 11 3.30
15: [3,] 12 2.25
16: [4,] 13 1.35
17: [5,] 14 0.62
18: [6,] 15 0.21
19: [7,] 16 0.08
20: [8,] 17 0.03
21: [9,] 18 0.01
22: [10,] 19 0.02
23: [11,] 20 0.01
24:
25: attr(,"class")
26: [1] "impvol"
27: >
上面列出了 s1 的 member variables,它包含 tick(是string obj),exp(是date obj),under(是 numeric obj),option (是 matrix),它的属性是 impvol object。借助于 class,我们可以很轻松的获取任意的股票数据。注意我们这个 class 其实是从 list 这个 class 的 derived,所以作为 derived class,就像 c++ 的inheritance 一样,它也具有 list 的属性。
然后我们定义 method,这里主要是作图,画implied volatility,这里也和 c++ 类似,我们需要 overload 一个已存在的函数 plot():
1: plot.impvol<- function(x, ...){
2: n <- nrow(x$option)
3: mtrty<-businessdaysbetween(from=sys.date(),to=as.date("2011-07-16"))/252
4: imvol <- array(na,n)
5: for ( i in 1:n){
6: result<-try(europeanoptionimpliedvolatility("call", x$option[i,2],x$under,x$option[i,1],0,0.02,mtrty,0.2),silent =true)
7: if(class(result) =="try-error") next
8: else {imvol[i]=europeanoptionimpliedvolatility("call", x$option[i,2],x$under,x$option[i,1],0,0.02,mtrty,0.2)$impliedvol}
9: }
10: result<-cbind(x$option[,1],imvol)
11: plot(result,col="2",main=paste("implied vol of", x$tick),xlab="strike",ylab="implied vol",xaxt = "n")
12: axis(1,at=x$option[,1],labels=t)
13: }
因为 plot 是一个 generic function, 我们用 plot.impvol 来 overload 它,注意在我们的 plot 函数里,我们实际上先计算了它的 implied vol。检视我们的 class 的method:
1: > methods(class="impvol")
2: [1] plot.impvol
测试我们的 method:
1: s1 <- impvol("f")
2: s2 <- impvol("goog")
3: s3 <- impvol("aapl")
4: s4 <- impvol("c")
5: par(mfrow=c(2,2))
6: plot(s1)
7: plot(s2)
8: plot(s3)
9: plot(s4)
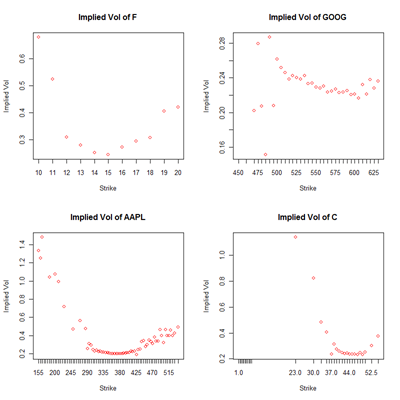
我们得到下面的 vol skew的 plot:
x 轴每一个 tick mark 都是一个 strike,如果那个 strike 对应的 implied vol 是 na,plot 自动就把那个数据点 drop 了。以 google 和 apple 为例,我们发现 deep ITM 的 call option 的 implied vol 有很多 missing values,并且还有异常的数值,其中的原因就是我们上面说的 liquidity 和 trading frequency的问题。最后一个 citi 的图,strike 在 $1 附近还有数据点,更能说明这个问题:这个数据源里还包括了citi并股前的数据。
OOP 大大简化了 R 的编程,所以学习 C++ 其实同时也很有助于 R 的使用,就像学点儿数学对于文科生也很有帮助一样:)
P.S. 因为编辑 CSS 出错,导致后半篇的字母全部被转化为小写 =_= 。




 前两天说起清代大臣的谥号,因为太忙没时间,未能尽言,现在有点儿空闲,多说两句。
前两天说起清代大臣的谥号,因为太忙没时间,未能尽言,现在有点儿空闲,多说两句。 一边 debug C++ codes,一边听昆曲《牡丹亭》,随便点开的是一出《怅眺》,末了一首联句很有趣:
一边 debug C++ codes,一边听昆曲《牡丹亭》,随便点开的是一出《怅眺》,末了一首联句很有趣: